CSP j/s初赛训练---数学知识
欢乐喷球:儿童游乐场有个游戏叫“欢乐喷球”,正方形场地中心能不断喷出彩色乒乓球,以场地中心为圆心还有一个圆形轨道,轨道上有一列小火车在匀速运动,火车有六节车厢。
假设乒乓球等概率落到正方形场地的每个地点,包括火车车厢。小朋友玩这个游戏时,只能坐在同一节火车车厢里,可以在自己的车厢里捡落在该车厢内的所有乒乓球,每个人每次游戏有三分钟时间,则一个小朋友独自玩一次游戏期望可以得到( )个乒乓球。假设乒乓球喷出的速度为2个/秒,每节车厢的面积是整个场地面积的1/20。

18
20
60
108
假设一台抽奖机中有红、蓝两色的球,任意时刻按下抽奖按钮,都会等概率获得红球或蓝球之一。有足够多的人每人都用这台抽奖机抽奖,假如他们的策略均为:抽中蓝球则继续抽球,抽中红球则停止。最后每个人都把自己获得的所有球放到一个大箱子里,最终大箱子里的红球与蓝球的比例接近于( )。
1:1
1:2
1:3
2:1
在一条长度为1的线段上随机取两个点,则以这两个点为端点的线段的期望长度是( )。
1/2
1/3
2/3
3/5
一家四口人,至少两个人的生日属于同一月份的概率是( )。
(假定每个人的生日属于每个月份的概率相同且不同人之间相互独立。)
1/12
1/144
41/96
3/4
小明要去南美洲旅游,一共乘坐三趟航班才能到达目的地,其中第1个航班准点的概率是0.9,第2个航班准点的概率为0.8,第3个航班准点的概率为0.9。如果存在第i个(i=1,2)航班晚点,第i+1个航班准点,则小明将赶不上第i+1个航班,旅行失败;除了这种情况,其他情况下旅行都能成功。请问小明此次旅行成功的概率是( )。
0.5
0.648
0.72
0.74
10000 以内,与10000互质的正整数有( )个。
2000
4000
6000
8000
一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?( )
20
21
22
23
分母是1001的最简分数一共有多少个?
120
240
360
720
某校六(1)班有学生45人,每人在暑假里都参加体育训练队,其中参加足球队的有25人,参加排球队的有22人,参加游泳队的有24人,足球、排球都参加的有12人,足球、游泳都参加的有9人,排球、游泳都参加的有8人,问:三项都参加的有多少人?
3
4
5
6
1副纸大小王4种花色,每种花色13张。假设从这52张牌中随机抽取13张纸牌,则至少( )张牌的花色一致。
2
3
4
5
在平面坐标系上任取n个整点(横纵坐标都是整数),其中一定存在两个点,它们连线的中点也是整点,那么n至少是几?
5
6
7
8
有35个球,红、白、黄各10个,另外有3个蓝色、2个绿色,试问无论如何取,至少取几个小球就能保证有4个同色球。
14
15
16
17
5种颜色的袜子各15只混装在箱子里,试问无论如何取,从箱子中至少取几只袜子,就能保证有3双袜子。(袜子无左右之分。)
7
8
9
10
有7个一模一样的苹果,放到3个一模一样的盘子中,一共有( )种放法。
7
8
21
37
甲、乙、丙三位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( )种。
36
48
96
192
将7个名额分给4个不同的班级,允许有的班级没有名额,有( )种不同的分配方案。
60
84
96
120
把8个同样的球放在5个同样的袋子里,允许有的袋子空着,共有( )种不同的分法?
(提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算同一种分法。
18
20
22
24
10个三好学生名额分配到7个班级,每个班级至少有一个名额,一共有( )种不同的分配方案。
56
72
84
504
相同与不同,空与不空问题。
盒子可空:
第1题 单选
(1)5个不同的小球放入3个不同的盒子(可有空盒),一共有多少种放法?
5
21
41
243
第2题 单选
(2)5个不同的小球放入3个相同的盒子(可有空盒)一共多少种放法?
5
21
41
243
第3题 单选
(3)5相同的小球放入3个不同的盒子(可有空盒)一共多少种放法?
5
21
41
243
第4题 单选
(3)5相同的小球放入3个相同的盒子(可有空盒)一共多少种放法?
5
21
41
243
相同与不同、空与不空问题。
盒子不能为空:
第1题 单选
(1)5个不同的小球放入3个不同的盒子(每盒不空),一共有多少种放法?
2
1+1=2
6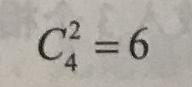
25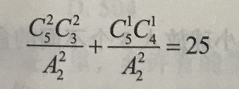
150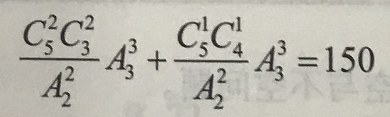
第2题 单选
(2)5个不同的小球放入3个相同的盒子(每盒不空),一共有多少种放法?
2
6
25
150
第3题 单选
(3)5个相同的小球放人3个不同的盒子(每盒不空),一共有多少种放法?
2
6
25
150
第4题 单选
(4)5个相同的小球放入3个相同的盒子(每盒不空),一共有多少种放法?
2
6
25
150
设含有10个元素的集合的全部子集数为S,其中由7个元素组成的子集数为T,则T/S的值为( )。
1/8
5/32
15/128
21/128
假设某个城市的车牌只有5位数字,每一位都可以取0到9。请问这个城市有多少个车牌倒过来恰好还是原来的车牌,并且车牌上的5位数能被3整除?( )
20
25
30
45
一些数字可以颠倒过来看,例如0、1、8颠倒过来还是它本身,6 颠倒过来是9,9颠倒来看是6,其他数字颠倒过来都不构成数字。
与此类似,一些多位数也可以颠倒过来看,比如 106 颠倒过来是901。假设某个城市的车牌只由5位数字组成,每一位都可以取0到9。
请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?( )
60
75
100
125
由数字1、1、2、4、8、8所组成的不同的4位数的个数是( )。
98
100
102
104
有5副不同颜色的手套(共10只,每副分左右手各1只),一次性从中取6只手套,请问刚好能配成两副手套的不同取法有( )种。
30
120
150
180
5个小朋友并排站在一列,其中有两个小朋友是双胞胎,如果要求这两个双胞胎必须相邻,则有( )种不同的排列方法。
24
36
48
72
从一个4X4的棋盘中选取不在同一行也不在同一列上的两个方格,共有( )种方法。
60
64
72
86